Hyperbolic Groups Presentation

We start with hyperbolic $2$-space, a real Riemannian $2$-mainfold denoted by $\mathbb{H}^2$ which has different isometrically diffeomorphic models.

Hyperbolic Models Revisited

Hyperboloid Model $\mathbb{I}^2$

Consider following bi-linear form in $\mathbb{R}^{3}$ :

and the upper fold of the hyperboloid associated to $\langle \cdot | \cdot \rangle$:

$\mathrm{I}^ 2$ is a smooth $2$-manifold with tangent space:

Since $\langle x | x \rangle = - 1$, the restriction of $\langle \cdot | \cdot \rangle$ to $\{ x \} ^ { \perp }$ is positive-definite.
Then it is a scalar product on $T _ { x } \mathrm{I} ^ { 2 }$ and hence gives a metric struture.

We shall denote by $\mathbb{I} _ 2$ the manifold $\mathrm{I} _ 2$ endowed with this metric structure.

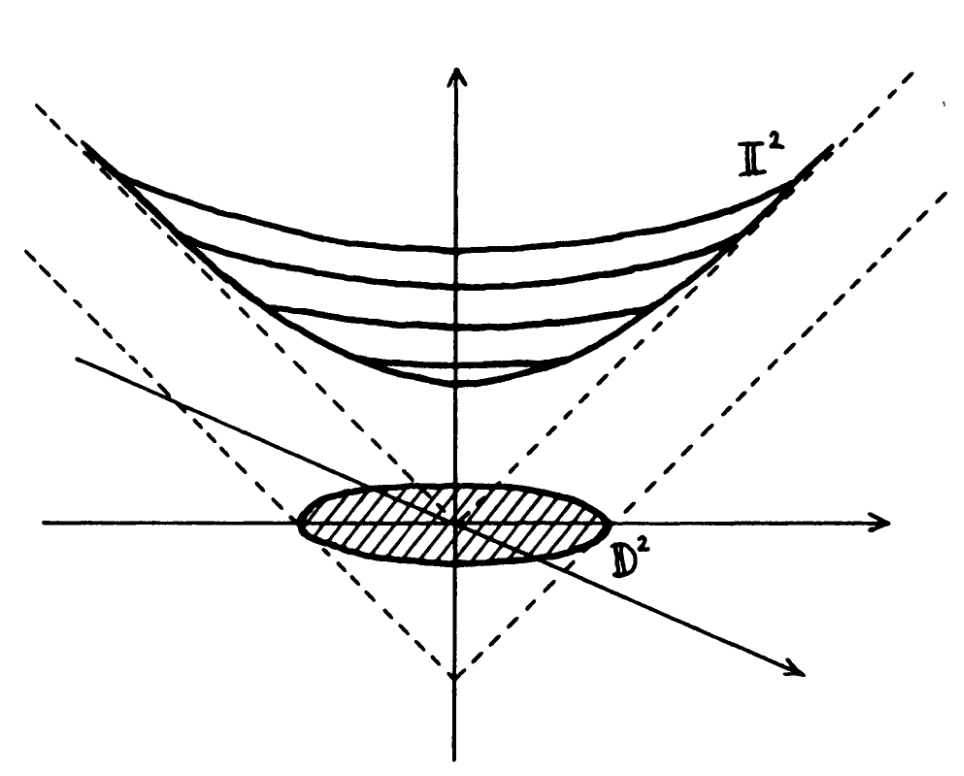
Disk Model $\mathbb{D}^2$

Disk model $\mathbb{D}^2$ comes from steographic projection of $\mathbb{I}^2$.

Dash lines indicate boundary of this projection.

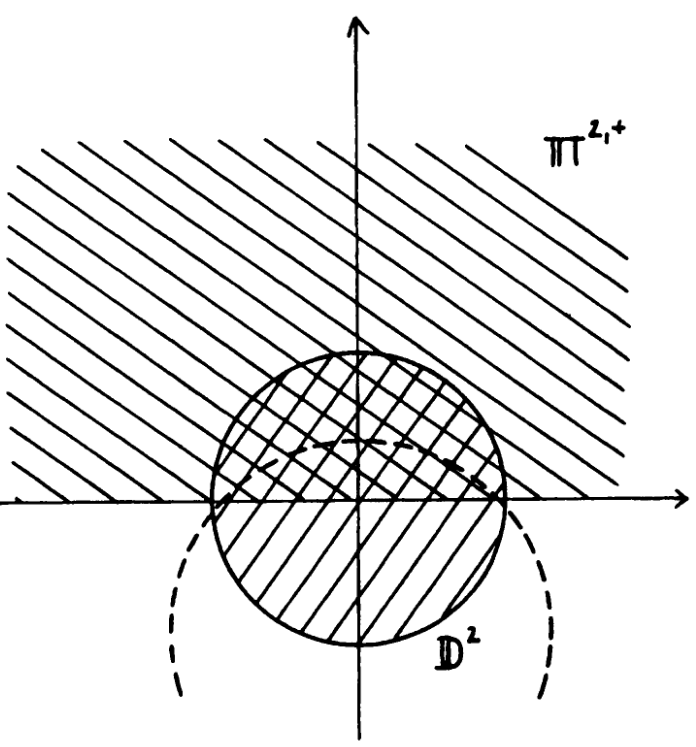
Half-Plane Model $\mathbb{\Pi}^2$

Half-space model comes from a Möbius transformation of $\mathbb{D}^2$.

It is a geometric inversion explained in the left picture: $OP\cdot OP^{\prime }=r^{2}$.

Isometry of $\mathbb{H}^2$

We admit following non-trival proposition

A sufficient condition for a diffeomorphism of $\mathbb{H}^{2}$ to preserve lengths is that it preserves angles.

We remark that

• it is trivial that length preserving implies angle preseving
• Möbius transformation is conformal, hence maps geodesics to geodesics in hyperbolic space
• this proposition is powerful and streamlines proofs in elementary hyperbolic geometry.

Now we land back to $\mathbb{H}^{2}$ and claim:

In disk model $\mathbb{D}^2$ and half-plane model $\mathbb{\Pi}^2$, geodesics are orthocircles, which are lines/circles perpendicular to the boundary.

Because half-plane $\mathbb{\Pi}^2$ is conformal to disk model $\mathbb{D}^2$, we only need to prove this for disk model $\mathbb{D}^2$.

• Diameters are fixed set of reflections hence are geodesics, they are perpendicular to boundary.
• Diameters are all geodesics passing the origin by uniquess of geodesics.
• After Möbius transformations that fix $\mathbb{D}^2$ we get all orthocircles from diameters.

Here we play a game to illustrate geodesics in disk model $\mathbb{D}^2$:
Spaceship in disk model $\mathbb{D}^2$.

Use Mathematica to interact with triangles in disk model $\mathbb{D}^2$.

$\delta$-Hyperbolicity

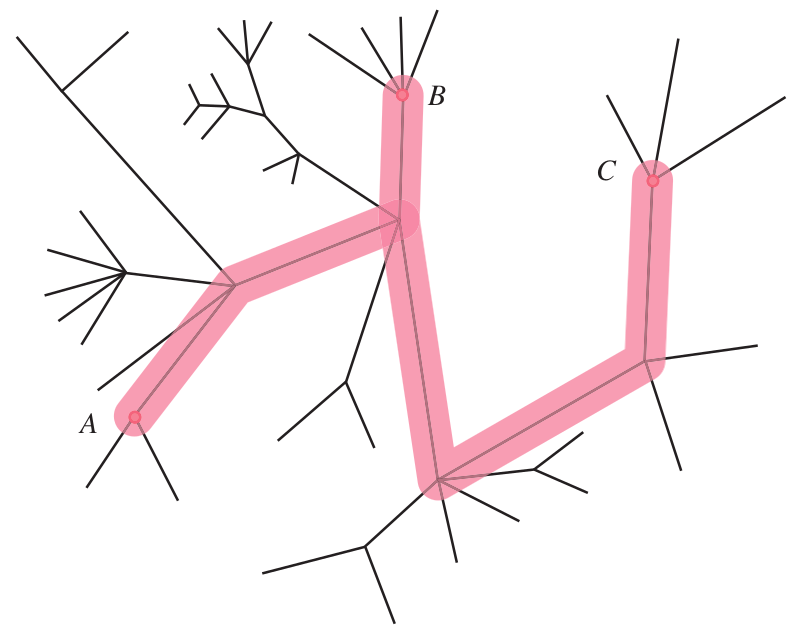
$\delta$-hyperbolicity is a property shared by geometrical trees and hyperbolic plane:

Triangles are thin.

A triangle is $\delta$-thin if each side is in the $\delta$-neighborhood of other two sides.

In the definition of $\delta$-hyperbolicity, the actual value $\delta$ is not important.

But we remark:

• In geometric trees, $\delta=0$, since $\overline{AC} \subset \overline{AB} \cup \overline{BC}$.

• What should the actual value of $\delta$ of hyperbolic plane?
  We can calculate this if we have time at the end.

Hyperbolic group

We claim without detailed verfication that:

$\delta$-hyperbolicity is invariant under quasi-isometry.

We apply this to get a definition:

• A finitely generated group is called hyperbolic if any of its Cayley graphs (for a finite generating set) is $\delta$-hyperbolicity.
• Well-defined since different finite generators give quasi-isometric Cayley graphs

Surface groups are hyperbolic

Surface groups are defined to be fundamental groups of hyperbolic surfaces.

• To define a hyperbolic surfaces / mainfold, we need to work with charts.
• This claim says that

  Hyperbolic surface has a hyperbolic fundamental group.

Add extra structure to manifold

A mainfold has chart in $\mathbb{R}^n$ with smooth coordinate transformation.
To generalize, we

1. allow charts to locate at a space form $X$
2. restrict coordinate transformation to be restriction of orientation-preserving isometry group $\mathcal{I}^+(X)$.
3. This defines a $(X, \mathcal{I}^+(X))$-manifold.

Example: torus is flat

We call an $(X, \mathcal{I}^+(X))$-manifold is

• hyperbolic, if $X=\mathbb{H}^n$
• elliptic, if $X=S^n$
• flat, if $X=\mathbb{R}^n$

We shall classify all surfaces soon.

Quotient manifold and Švarc–Milnor lemma

1. A $(X, \mathcal{I}^+(X))$-manifold $M\cong X/\pi_ 1 (M)$ as Riemmanian manifold
2. $\pi_ 1(M)$ is quasi-isometric to $X$

3. It follows

   Hyperbolic surface has a hyperbolic fundamental group.

4. We then want to find out hyperbolic surfaces, that is to say,
   a geometric classification of surfaces.

Geometric classification of surfaces

We always assume closed, oriented and connected surface / $2$-manifold.

Elliptic surface

$2$-Sphere is the only elliptic surface since every element of $\mathcal{I}^{+}(S^2) = SO(3)$ has fixed points, which forces elliptic surfaces as quotient manifold of $S^2$ to be trivial.

Flat surface

We have shown torus in Mathematica

Hyperbolic surface

Surface with genus bigger than 2, i.e., connected sum of $n$-torus (with $n \ge 2$) are hyperbolic.
Prove by JavaScipt Code.

Bonus (if we have time)

• Actual value of $\delta$ of hyperbolic plane is $\tanh^{-1}(1/\sqrt2)=\log(1+\sqrt2)$.

  • In disk model, move triangle to contain the origin then vertices are on radius, endpoints of three radius form an ideal triangle containing the original triangle.
  • Any ideal triangle is enough to conclude since Möbius transformation is 3-transitive.
  • We only need to cover one side of ideal triangle by the same reason above, to simplify put it in half plane model.
  • Finally our problem reduces to finding distance of a midle-point to another side. Use reflection.

• A snake game on $2$-torus $\mathrm{T}^2$

Appendix and notes (out of presentation)

Formal definition of $(X,G)$-structure

Let $A$ be a connected, simply connected, oriented $n$-dimensional manifold($n\ge 2$), and let $G$ be a group of diffeomorphisms of $A$ onto itself; we shall say a differentiable $n$-manifold $Μ$ is endowed with an $(X,G)$-structure if we are given an open covering $\{U_ i\}$ of $M$ and a set of differentiable open mappings $\{\varphi_ i\}$ (with $\varphi_ i : U_ i \mapsto X$) such that

1. $\varphi_ i : U_ i \mapsto \varphi_ i(U_ i)$ is a diffeomorphism;
2. if $U_ i \cap U_ j \ne \emptyset$ then the restriction of $\varphi_ i \circ \varphi_ {j}^{-1}$ to each connected component of $\varphi_ j(U_ i \cap U_ j)$ is the restriction of an element of $G$.

$\{(U_ i , \varphi_ i )\}$ will be called an atlas defining the $(X,G)$-structure.

Classfication using complex analysis

This classfication corresponds to uniformization theorem about simply connected Riemannian surfaces.

• Any surface has isothermal coordinate.
• Isothermal coordinate gives a complex structure on this surface.
• Universal covering of a Riemannian surface is a simply connected Riemannian surface.
• There are only three possible simply connected Riemannian surfaces: $\hat{\mathbb{C}}$, $\mathbb{C}$ and $\mathbb{D}$.
• These three possibilities correspond to elliptic, flat and hyperbolic surfaces.
• Details are in Dynamics in One Complex variable, chapter 1, section 2, third edition by John Milnor.

Notes

• Uniquess of geometric classification comes from Gauss-Bonet theorem and trianglization of surfaces.
• Another proof of hyperbolic surfaces uses pant decomposition of $n$-torus $\mathrm{T}^n$ (with $n \ge 2$). See Reimannian Geometry, section 3.L.4 compact surfaces, third edition, by Sylvestre Gallot, Dominique Hulin and Jacques Lafontaine.